3D Transformations in CGLibPy:
3D Transformations is an essential part of Computational Geometry. Any CG Library without transformations is incomplete. As a rule, CGLibPy is a Computational Geometry which considers every geometry a 3D object. Hence, the transformations can’t be restricted only to 2D operations. Transformations in CGLibPy will take a generalized approach where a geometry is moved in a 3D world at any given moment.
Transformation essentially means, change in the state of given geometry. This change of state in 3D world can be done by Translation (Linear Movement), Rotation, Scaling, Shear (Skew) etc.
In CGLibPy, there is a separate class created called CGLibPy_TransF which will be used to store the transformation.
import math
class CGLibPy_TransF(object):
translateXYZ = []
transDist = 0
transVec = [1,0,0]
transByXYZ = True
rotAng = 0
rotPt = [0,0,0]
rotVec = [0,0,1]
scaleVec = [1,1,1]
xShear = [1,1]
yShear = [1,1]
zShear = [1,1]
transType = 0 # 0 = Translation, 1 = Rotation, 2 = Scaling, 3 = Shearing
# Translation in X, Y and Z Directions
def setTranslationXYZ(self,dx=0,dy=0,dz=0):
self.transByXYZ = True
self.translateXYZ = [dx,dy,dz]
self.transType = 0
# Translation along a vector by given distance
def setTranslationVec(self,dist=0,vec=[1,0,0]):
self.transByXYZ = False
self.transDist = dist
self.transVec = vec
self.transType = 0
# Rotation around and axis and point of rotation
def setRotation(self,ang=0,rotPt=[0,0,0],rotVec=[0,0,1]):
self.rotAng = math.radians(ang);
self.rotPt = rotPt
self.rotVec = rotVec
self.transType = 1
# Scaling along X, Y and Z directions
def setScaling(self,scaleX=1,scaleY=1,scaleZ=1):
self.scaleVec.append(scaleX)
self.scaleVec.append(scaleY)
self.scaleVec.append(scaleZ)
self.transType = 2
# Shearing Factors along X, Y and Z Directions
def setShear(self,xShear=[1,1],yShear=[1,1],zShear=[1,1]):
self.xShear = xShear
self.yShear = yShear
self.zShear = zShear
self.transType = 3
Remember that in CGLibPy we handle only ONE transformation at a time.
Please not that, ALL CGLibPy Transformations are in-place transformations, which means that transformation methods will change the coordinates of the actual geometry and will NOT return any new geometry!
So, for example if you want to scale and rotate the geometry you will have to create a transformation class CGLibPy_TransF object, setScaling() then apply the scaling on the geometry and then setRotation() then apply the rotation on the geometry.
# Define a geometry line1 = CGLibPy.CGLibPy_Line([0,0,0,1,1,1]) # Define transformation tr1 = CGLibPy.CGLibPy_TransF() # First Transformation - Translation along X Y and Z axes tr1.setTranslationXYZ(5,5,5) line1.transformBy(tr1) #Second Transfomration - Rotate around a point around a vector tr1.setRotation(self,15,[2.5,1.2,5],[0.7071,0.7071,0] line1.transformBy(tr1)
3D Translation in CGLibPy:
Translation in CGLibPy is handled in two different ways,
- Linear movement along X, Y and Z Axes directions by given distances respectively
- Linear movement along a given vector V by given distance
Translation Along X, Y and Z Axes:
# Define a geometry line1 = CGLibPy.CGLibPy_Line([2.5,4.5,1,2,4,1.5]) # Define transformation tr1 = CGLibPy.CGLibPy_TransF() # Translation along X Y and Z axes tr1.setTranslationXYZ(10,20,-10) # Apply the Transformation line1.transformBy(tr1)
This type of translation requires user to input three distances (scalar values) along X, Y and Z axes direction respectively. The CGLibPy geometry will be moved “Translated” by these distances along X, Y and Z axes. CGLibPy_TransF has a method to set this kind of translation as setTranslationXYZ(dx, dy, dz) where dx, dy and dz are scalar values or distances along X, Y and Z axis respectively.
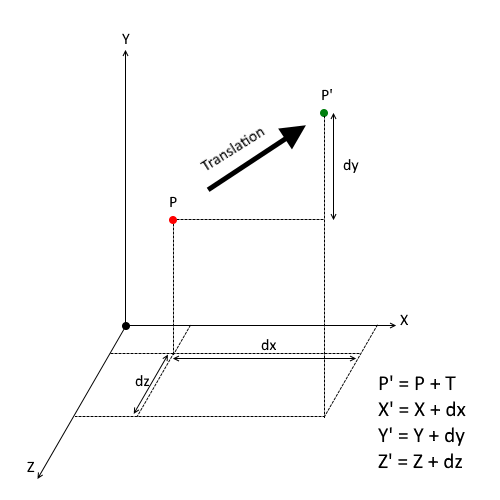
Translation Matrix 4×4:
Although, we are not directly using 4×4 matrix for translation following matrix manipulation will help you understand the Transformation of a Point P from it’s current location to Point P’
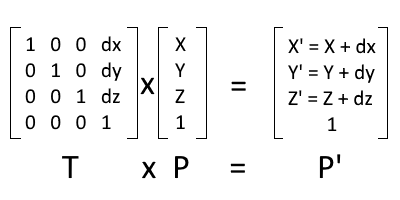
Translation Matrix 3×3:
In CGLibPy, currently we are using 3×3 matrix calculation for Translation of the Point. While implementing Translation using 3×3 matrix, instead multiplication of of matrices, we will do Addition of the Matrices which is much simpler and faster operation.
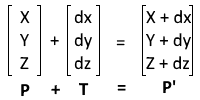
So setTranslationXYZ(dx, dy, dz) will Translate a Geometry by distance dx, dy and dz in X, Y and Z axis directions respectively.
Translate Along a Vector in 3D:
# A CGLibPy Arc geometry c1 = CGLibPy.CGLibPy_Point(1,1,1)#Centre rad1 = 5.0 #Radius arc1 = CGLibPy.CGLibPy_Arc([c1,rad1,True]) # CGLibPy Transformation tr2 = CGLibPy.CGLibPy_TransF() # Translation by 2.5 Along Unit Vector [0.956,0.27,-0.1156] tr2.setTranslationVec(2.5,[0.956,0.27,-0.1156]) # Apply the transformation arc1.transformBy(tr2)
Another way of Translation available in CGLibPy is Translation Along a Vector. Normally translation is done along X, Y and Z axes but, sometimes there is a need to move the geometry linearly along a unit vector. Some of the possible applications can be Robotics, CAM etc.
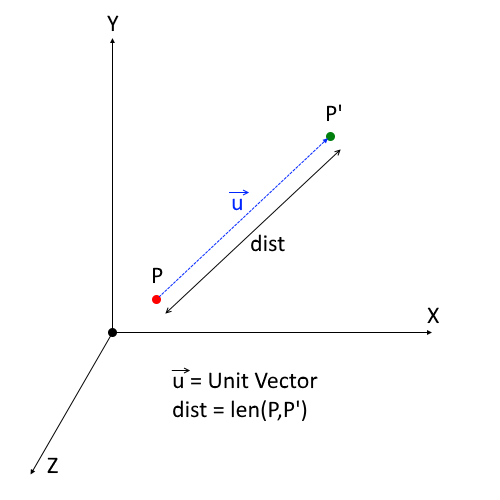
In the example mentioned above user will have to use setTranslationVec(dist, vec) method where, dist is the distance by which we need to move and vec is the direction vector. Mathematically speaking, translation along a unit vector by given distance is nothing but multiplication of a scalar value and the unit vector.
Note: We have used this technique in Parametric Equation of Line while Finding coordinates of a point along a vector at a given distance!
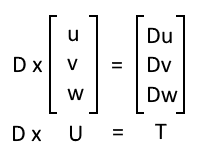
Once the translation vector is formulated the matrix manipulation is same as mentioned above in translation along X, Y and Z axes.
3D Rotations in CGLibPy:
CGLibPy believes that real world is 3D hence, everything computed must satisfy the 3D world mathematics. Rotation is no exception to this philosophy. In CGLibPy we consider only the rotation axis and rotation point while rotating a geometry. This rotation axis can be any vector in the 3D space and rotation point any 3D point about which the geometry will be rotated.
Rotation Matrix in CGLibPy:
Ultimately it is the matrix manipulation which determines the final location and position of the geometry. Let’s consider that we are given rotation angle as θ (degrees), rotation axis as V and point of rotation as P.
# CGLibPy Geometry line2 = CGLibPy.CGLibPy_Line([2.5,-3.0,-1.24,12,-19.4,-4.56]) # CGLibPy Transformation tr3 = CGLibPy.CGLibPy_TransF() # Setting rotation angle = 25 degree, Rotation Point [2,2.5,-3] and rotation vector [-0.956,-0.27,0.1156] tr3.setRotation(25,[2,2.5,-3],[-0.956,-0.27,0.1156]) # Apply the Rotation line2.transformBy(tr3)
Then, the sequence of matrix manipulation is as follows,
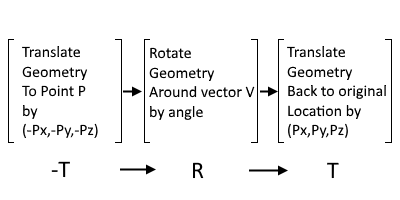
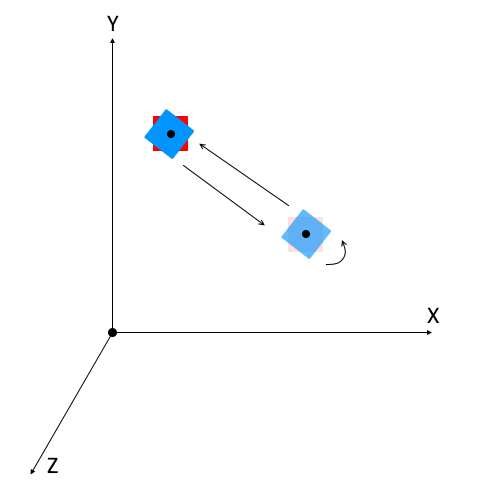
Sequence of Transformation
The Rodrigues’ Rotation Formula:
CGLibPy used generalized rotation matrix which only needs rotation angle and rotation vector The Rodrigues’ Rotation Formula
Tmat = (cosθ)V + (1 – cosθ)(K . V)K + sinθ (K x V)
Where,
θ = angle of rotation
K = Unit vector as axis of rotation
V = Vector (Coordinates) to be rotated
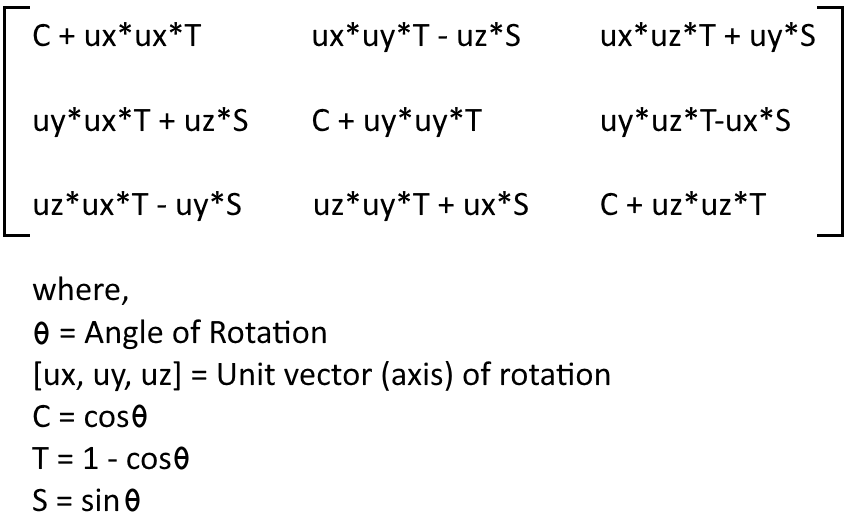
3D Scaling In CGLibPy:
CGLibPy handles Scaling in a very simple way. User just needs to define scaling factors for X, Y and Z directions
# CGLibPy Points for Rectangle p1 = CGLibPy.CGLibPy_Point(10,5,20) p2 = CGLibPy.CGLibPy_Point(20,5,20) p3 = CGLibPy.CGLibPy_Point(20,15,20) p4 = CGLibPy.CGLibPy_Point(10,15,20) # CGlibPy Rectangle rect1 = CGLibPy.CGLibPy_Rectangle([p1,p2,p3,p4]) # CGLibPy Transformations tr4 = CGLibPy.CGLibPy_TransF() # Set Scaling tr4.setScaling(2.5,1.25,3.4) # Apply Transformation rect1.transformBy(tr4)
Scaling by definition means scalar multiplication of the coordinates. CGLibPy handles scaling in X, Y and Z axes. Scaling Matrix 3×3 in CGLibPy looks like,
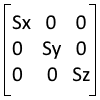
Where Sx, Sy and Sz are scaling factors along X, Y and Z axis respectively. So, after multiplication of this scaling matrix and coordinates of the point P (Xp, Yp, Zp) becomes (Sx*Xp, Sy*Yp, Sz*Zp)
Default scaling factor considered in CGLibPy is 1.
3D Shear In CGLibPy
Just as scaling, shear transformation is handled in a straight forward way in CGLibPy
# Points for a polygon p1 = CGLibPy.CGLibPy_Point(0,0,20) p2 = CGLibPy.CGLibPy_Point(-5,2,20) p3 = CGLibPy.CGLibPy_Point(-1,3,20) p4 = CGLibPy.CGLibPy_Point(6,7,20) p5 = CGLibPy.CGLibPy_Point(10,0,20) p6 = CGLibPy.CGLibPy_Point(4,-3.5,20) # CGLibPy Geometry - Polygon poly1 = CGLibPy.CGLibPy_Polygon([p1,p2,p3,p4,p5,p6]) # CGLibPy Transformation tr4 = CGLibPy.CGLibPy_TransF() # Apply Shear Factors tr4.setShear([-1.5,1],[0.23,0.4],[0.125,-1.35]) # Apply Shear Transformation poly1.transformBy(tr4)
Shear transformation in 3D is nothing but addition of a given coordinate with scalar multiplications of other two coordinates with shear factors. The Shear matrix in 3D looks like,

Where, S’s are shear factors along X, Y and Z axes for each coordinate. The new coordinates or coordinates after shear transformation can be found out as,
P’ = T*P
Hence,
X’ = X + Sxy*Y + Sxz*Z
Y’ = Y + Syx*X + Syz*Z
Z’ = Z + Szx*X + Szy*Y
Note: The default shear factors are kept as zero in CGLibPy.