Vector Algebra

Vector Algebra is a branch of mathematics which deals with mathematical operations of vectors. It is The Foundation of Computational Geometry. Let’s go through the vector operations one by one.

Vector Addition:

Vector addition by name means addition of coefficients of vectors. Let’s consider following vectors

a = a1i + b1j + c1k

and

b = a2i + b2j + c2k

then, vector addition is given as,

(a+b) = (a1+a2)i + (b1+b2)j + (c1+c2)k

Graphically vectors are added using a Parallelogram Rule, where two distinct vectors when offset form a Parallelogram and Vector Addition is nothing but the Diagonal, with starting Point of fist vector as starting point and End Point of other vector as end point.

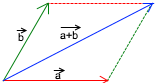
Vector Subtraction:

Vector Subtraction is nothing but modified vector addition. For example if we have two vectors as,

a = a1i + b1j + c1k

and

b = a2i + b2j + c2k

(a-b) = (a + (-b))

where,

-b = -a2i -b2j -c2k

then, vector subtraction is given as,

(a-b) = (a1-a2)i + (b1-b2)j + (c1-c2)k

which is nothing but (a-b) = (a + (-b))

Graphically Speaking, it is nothing but Other Diagonal of the Parallelogram formed by given vectors.

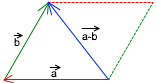
Scalar Product/Multiplication:

A scalar value is just a magnitude without any directions. Scalar Product output is scalar multiplication of coefficients with a scalar value. Let’s consider a vector as

vec = ai + bj +ck

and a scalar value ‘m’ then,

scalar multiplication is,

m*vec = (m*a)i + (m*b)j + (m*c)k

Basically Scalar multiplication is nothing but scaling of the given vector i.e. scaling of magnitude. Graphically it can be shown as following,

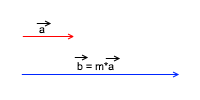
Dot Product:

The dot product between two vectors gives a scalar value as output. The dot product is nothing but the sum of product of coefficients of given vectors. Let’s consider two vectors,

a = a1i + b1j + c1k

and

b = a2i + b2j + c2k

then, Dot Product is,

a.b = |a|*|b|*cosθ

where, |a|, |b| are magnitudes of vectors a and b and θ is the angle between two vectors.

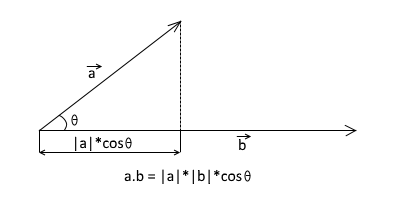
Dot Product can also be represented as follows,

a.b = (a1*a2) + (b1*b2) + (c1*c2)

Computational Geometry Library in Python – Dot Product:

def dotProduct3DIJK(I1,J1,K1,I2,J2,K2):
    dp = I1*I2 + J1*J2 + K1*K2 
    return dp

Cross Product:

Cross product is technically Vector Product and is very useful while working in 3-dimensional Computations. The primary difference between Dot Product and Cross Product is that output of Cross Product is another vector. Output vector of the cross product is perpendicular to both the planes.

The direction of this vector is determined by Right-Hand Thumb Rule, i.e. if forefinger shows the direction of the first vector and middle finger shows the direction of the second vector, extended thumb determines the direction of the Cross Product. (Sometimes, right-hand thumb rule considers rolled fingers. If rolled fingers show the direction from the first vector to the second vector then, extended thumb shows the direction of Cross Product)

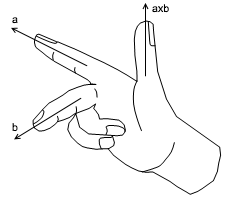
Let’s consider two vectors,

a = a1i + b1j + c1k

and

b = a2i + b2j + c2k

then, Cross Product is,

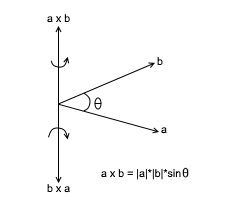
axb = |a|*|b|*sinθ

where, |a|, |b| are magnitudes of vectors a and b and θ is the angle between two vectors. Cross Product can also be represented as

axb = (b1*c2 – c1*b2)i + (c1*a2 – a1*c2)j + (a1*b2 – b1*a2)k

Computational Geometry Library in Python – Cross Product:

def crossProduct3DIJK(I1,J1,K1,I2,J2,K2):
    a = J1*K2-K1*J2
    b = K1*I2-I1*K2
    c = I1*J2-J1*I2
    cp = [a,b,c]
    return cp

Check if Lines are Perpendicular or Parallel:

Once you understand the concepts of the dot product and the cross product, it becomes very easy to check if given vectors are parallel or perpendicular to each other. Let’s see how we can use the dot product and cross product to determine it.

Perpendicular Lines:

The dot product of two vectors a and b is given as,

a.b = |a|*|b|*cosθ

We all know,

cosθ = 0 when, θ = π/2 or 3π/4

Hence, it is evident that vectors a and b are perpendicular to each other when a.b = 0 

Please check how it handled in CGLibPy

# vec1 and vec2 are direction vectors
def areVectorsPerpendicular(vec1,vec2):
    dP = dotProduct3D(vec1,vec2) 
    if(math.isclose(dP,0.0)):
        return True
    else:
        return False

Parallel Lines

The cross product of two vectors a and b is given as,

axb = |a|*|b|*sinθ

We all know,

sinθ = 0 when, θ = 0 or 2π or π

Hence, it is evident that vectors a and b are parallel to each other when axb = 0 

Please check how it handled in CGLibPy

# vec1 and vec2 are direction vectors
def areVectorsParallel(vec1,vec2):
    cP = crossProduct3D(vec1,vec2)
    vecLen = math.sqrt(cP[0]*cP[0] + cP[1]*cP[1] + cP[2]*cP[2])
    if(math.isclose(vecLen,0.0)):
        return True
    else:
        return False

Angle Between Two Vectors:

One of mostly asked and an important question asked by students of Computational Geometry is “How to find an angle between two vectors?” I have a good news for you, there is only one solution to following questions…

1. How to find the angle between two vectors in 2D or in 3D?
2. How to find the angle between two lines in 2D or in 3D?

Let’s consider two vectors,

a = a1i + b1j + c1k

and

b = a2i + b2j + c2k

we know now that, the Dot Product is,

a.b = |a|*|b|*cosθ where

θ is angle between two vectors

Then,

cosθ = (a.b)/(|a|*|b|)

Hence,

θ = arccos((a.b)/(|a|*|b|))

Just like we saw how to find angle between two vectors we can find angle between two lines, using direction vectors of given lines!

Which Side of Line Point Lies:

A very common question that anyone who tries to implement any Computational Geometry algorithm, asks is “On which side of the line a point lies?” or “How to find is a point lies on Left or Right side of the line?” or “Point lies on which side of the line?”

Similarly, the solution to this problem will also give use answer to the question “Find the Orientation (Clockwise or Counter Clockwise) from any given three sequential points”

It is very simple to find “The SIDE on which a point lies w.r.t. given line”.

Let’s consider Line L between two Points P₀ (x₀,y₀) and P₁ (x₁,y₁) ,

The direction vector of this line U can be represented as,

U = ai + bj

where,

a = x₁-x₀

b = y₁-y₀

Let’s consider point P (x,y) be any point.

Then, we will create a vector V from point P₀ to P as,

V = li + mj

where,

l = x-x₀

m = y-y₀

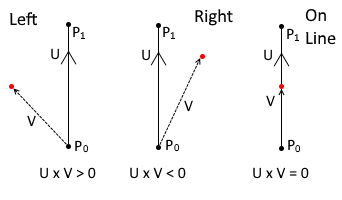
Now, we will use Cross Product of UxV  to determine on which side point lies. The Determinant of this cross product can be used to find if Cross Product is +ve or -ve.

Determinant  = (a*m)-(b*l)

So,

Determinant = (x₁-x₀)*(y-y₀) – (y₁-y₀)*(x-x₀)

If Determinant > 0 then, point P lies on LEFT side of the Line

If  Determinant < 0 then, point P lies on RIGHT side of the Line

If  Determinant = 0 then, point P lies ON the Line

Notes:

Graphically speaking if the Cross Product vector direction is UP then the Point lies on the Left side of the Line else if Cross Product vector direction is DOWN then the Point lies on the Right side of the line. This direction of the vector can be found out by Right-Hand Thumb Rule.

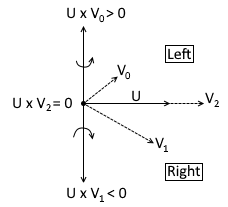
Orientation From Three Points

Also, this code can be used to determine the Orientation from any given three points. If points P₀ , P_{1 ,} P₂ are given sequentially, then the Orientation Clockwise or Counter Clockwise can be determined based on which side point P₂ lies w.r.t. Line/Vector created by P₀ and P₁. If the Cross Product is magnitude is Zero (0) then three points are Collinear.

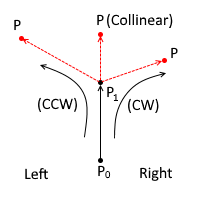
Computational Geometry Library in Python – Clockwise or Counter Clockwise Orientation:

def ccwWithDet(d1,d2,d3,d4):
    #Left or CCW side
    if (d1*d4 > d2*d3):
        return 1
    #Right or CW side
    if (d1*d4 < d2*d3):
        return -1
    #On the line
    return 0 

def ccwOrcwXY(point0,point1,point2):
    dx1 = point1.X - point0.X
    dy1 = point1.Y - point0.Y
    dx2 = point2.X - point0.X 
    dy2 = point2.Y - point0.Y
    return ccwWithDet(dx1,dy1,dx2,dy2)