Parametric Equation

Parametric Equation

Parametric Equation is a very useful representation of curves in Computational Geometry. Every geometry is a set of infinitely many points serially places along a specific pattern viz equation of the curve. Parametric Equation is a function of one or more parameters which will represent coordinates of all the points along the curve. So, coordinates of any point along the curve can be found out by simply replacing the parameter/s by their values.

So, for any given curve ‘C‘ the Parametric Equation can be expressed in terms of a parameter ‘t‘ like,

C = ƒ(t)

Now, coordinates of the points along curve C can be represented by following Parametric Equation

C_p (t)= (x(t), y(t), z(t))

Which means that, X,Y, and Z Coordinates of any point can be found by replacing t  with value within its range. Let’s see parametric equations of some of the most commonly used geometries in Computational Geometry.

---

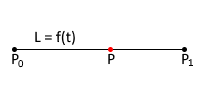
Parametric Equation of Line

Parametric Equation of Line is,

P = P₀ + (P₁-P₀)*t

where, P = Point on the Line, P0 = Start Point, P1 = End Point, t = Parameter

This Parametric Equation can be extended to find coordinates of any point P on the line as follows,

Xp = X₀ + (X₁-X₀)*t

Yp = Y₀ + (Y₁-Y₀)*t

Zp = Z₀ + (Z₁-Z₀)*t

Another question that gets asked all the time is “How to find coordinates of a point at a distance from starting point on the line?” or “How to find coordinates of point at a distance from a point along a vector?” The solution as below,

From the parametric equation of the line mentioned above we can see that (P₁-P₀) is nothing but the Direction Vector of the given line. A direction vector is represented as,

u = P₁-P₀

⇒ u = Ai + Bj +Ck

where,

A = x1-x0

B = y1-y0

C = z1-z0

So, first step to be done is Normalizing the Direction Vector

û = ai + bj + ck where,

a = (A/L)

b = (B/L)

c = (C/L) and,

L = Length of the vector = √(A)² + (B)² + (C)²)

which is also equal to the length of the Line segment between points P₀ ,P₁

L = Length of the Line Segment = √(x1-x0)² + (y1-y0)² + (z1-z0)²)

Now, Let’s try to find coordinates of a Point P at a distance d from a given Point P₀ along vector u. According to the Parametric Equation of the Line

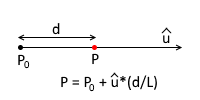
P = P₀ + (u)*t

Now, the parameter t = (distance from the start Point)/(Vector Length or Length of the Line Segment)

∴ t = d/L

So, coordinates of Point P can be found out as follows,

X_p = a*(d/L)

Y_p = b*(d/L)

Z_p = c*(d/L)

Notes :

Here are are some points to be remembered while using Parametric Equation of the Line

• Parameter t = 0 at the start point
• Parameter t = 1 at the end point
• If t < 0 or t > 1 then, point lines on the line but outside the bounds of start point and end point
• If t < 0 then, point lies before start point
• If t > 0 then, point lies after the end point
• Parameter t is nothing but ratio of directional distance of a point from start point to the length of the line
  • t = ±Length(P₀ ,P) / Length(P₀ ,P₁)

---

---

Parametric Equation of Arc

Parametric Equation of an Arc is,

P = C + R*ƒ(t)

where, P = Point on the arc, C = Centre of the arc, R = Radius of the arc and ƒ(t) = Parametric Function.

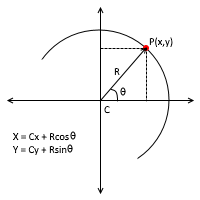
This Parametric Equation the Arc can be extended to find the coordinates of any point P on the Arc as follows,

Xp = Cx + R*cos(2πt)

Yp = Cy + R*cos(2πt)

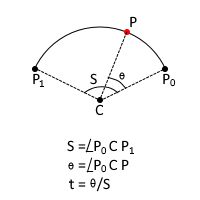
Please Note:

• For Full Circle the parameter t is the angle θ
• For an Arc t is the ratio of rotation angle from start point of an arc θ to total sweep angle S

Parametric Equation of 3D Circle:

Parametric Equation of the 3D Circle is given as,

P = R*cos(t)u + R*sin(t)n × u + C

where,

P = Any point on Circle,

R = Radius of Circle,

C = Centre of Circle,

n = Axis of Circle,

u = A unit vector from C toward a point on the circle

t = Parameter

Now, if we consider the orientation of the circle (angle made by axis of the circle) is specified by the

azimuth angle ∅ ∈ [-π,π]

and

the zenith angle θ ∈ [0,π]

n = [cos∅ sinθ , sin∅ sinθ , cosθ]

u = [-sin∅ , cos∅ , 0]

so,

nxu = [cos∅ cosθ , sin∅ cosθ , -sinθ]

Notes :

Here are are some points to be remembered while using Parametric Equation of the Arc

• Parameter t = 0 at the start point
• Parameter t = 1 at the end point
• If the Parameter t is > 1 then, it just means that the coordinate will be found after completing a whole circle at parameter value t = t – 1
• If the Parameter t is -ve, it represents Clockwise Orientation (CW) and if it’s +ve then, it represents Counter Clockwise Orientation (CCW)

---

Parametric Equation of Ellipse

Parametric equation of Ellipse if (Xc, Yc) is centre of the Ellipse and Major Axis is parallel to X-Axis and a,b = semi axis length Major and Minor respectively is

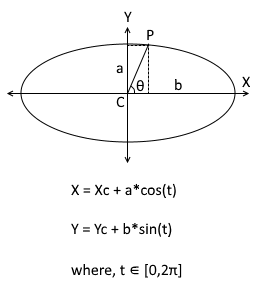
X = Xc + a*cos(t)

Y = Yc + b*sin(t)

where, t ∈ [0,2π]

Parametric equation of Ellipse if (Xc, Yc) is centre of the Ellipse and Major Axis is at an angle φ w.r.t. X-Axis and a,b = semi axis length Major and Minor respectively is

X = Xc + a*cos(t)*cos(φ) – b*sin(t)*sin(φ)

Y = Yc + a*cos(t)*sin(φ) + b*sin(t)*cos(φ)

where, t ∈ [0,2π]