Introduction

Every entity in Computational Geometry is defined in space using it’s position. This position is relative to an imaginary location called Origin. Positions are measured along imaginary mutually perpendicular vectors which originate from origin which are called Axes. These are X, Y and Z axes. Most of the algorithms are first developed in either 2 dimensions (2D) or 3 dimensions(3D). There are two types of coordinates systems

1. World Coordinate System : This is the coordinate system where, origin of the system is absolute origin or world origin (0,0,0). Which means a position at distance 0 along X, Y and Z axis respectively.
2. Local Coordinate System : This is the coordinate system where, new relative origin is assumed w.r.t. world origin and three mutually perpendicular vectors originate from this local origin. This coordinate system is defined using a transformation matrix. 

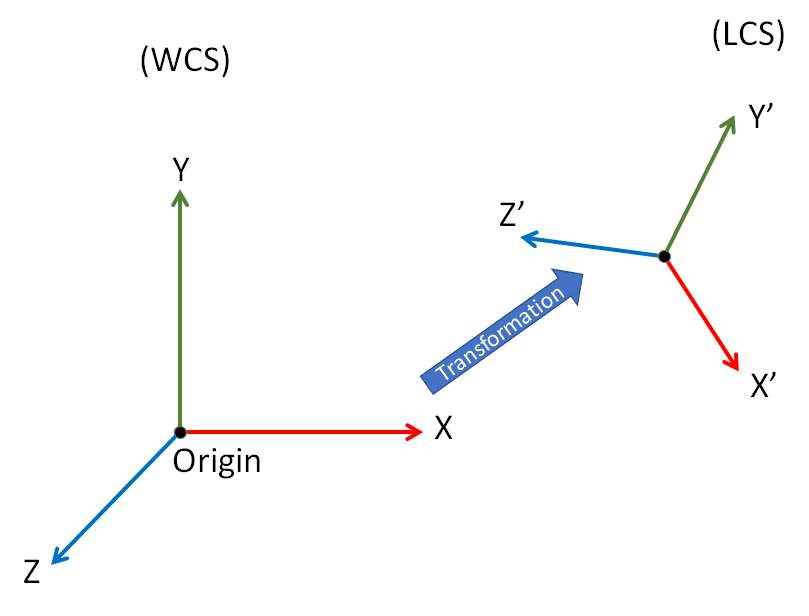
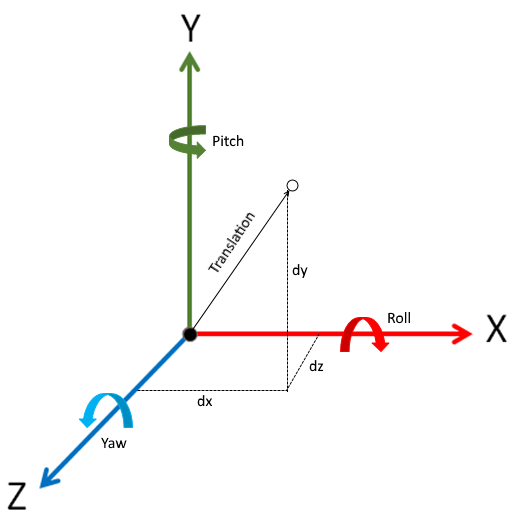
Transformation matrix is basically combination of rotations around X,Y and Z axes and translation i.e. movement by certain distances along these axes.

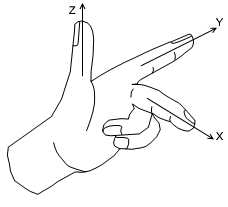
Usually applied Coordinate System in Computational Geometry is defined by Left Hand System , where Thumb, Forefinger and Middle finger are extended where these fingers are mutually perpendicular to each other.

 

Transformations are especially used in cased of CAD/CAM and also during animations. For examples if you want create a video game where the user is a pilot of a plane then, the airplane must rotate, move and turn according to the user’s inputs. This is nothing but transformations applied on the airplane model.