Line

After Point line is another basic geometry used in Computational Geometry. A line is defined as infinite set of points in a line extending in both directions towards infinity. Line has only one dimension, length. Points which fall on a given line are defined as Collinear Lines.

Computational Geometry Library in Python – Line:

class CGLibPy_Line(object):
    startPt = None
    endPt = None
    midpt = None
    vec = None
    lineLen = 0.0

    def __init__(self,_args):
        if len(_args) == 2: # Two Points
            self.startPt = _args[0]
            self.endPt = _args[1]
        elif len(_args) == 6: # Six Coordinates
            self.startPt = CGLibPy_Point(_args[0],_args[1],_args[2])
            self.endPt = CGLibPy_Point(_args[3],_args[4],_args[5])

Let’s look at following image, there is line L and a point P is on the line. The line extends in both directions infinitely.

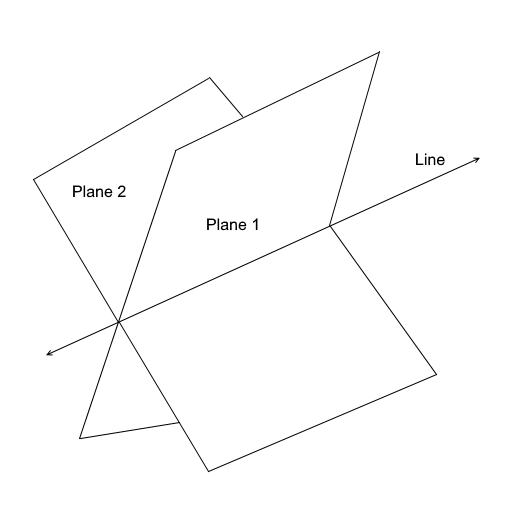
Another definition of line is that, A Line is defined by intersection of two infinite planes.

Line Segment:

While learning Computational Geometry it is necessary to understand the difference between a Line and A Line Segment. A Line segment is essentially a segment or a portion of a line. This line segment is defined as a subset of a line between any given two distinct points.

Hence, line segment has a Start Point and an End Point. Because of the definition of start and end, a line segment has a specific direction. This direction is determined by the direction vector. (We will cover Vectors in later chapters). Also, the length of the line segment is the distance between start point and end point of the line.

Let’s consider point P1(x1,y1,z1) is start point and P2(x2,y2,z2) is the end point of given line segment. Then,